Mạch OR
Thứ ba - 22/01/2013 22:58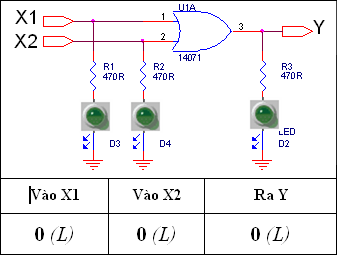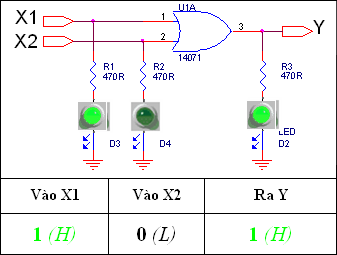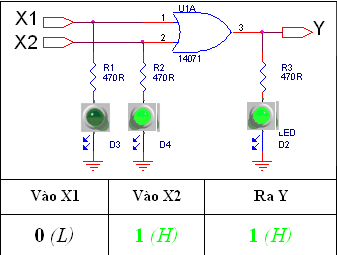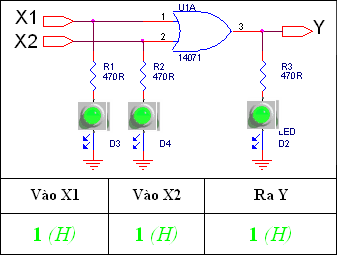
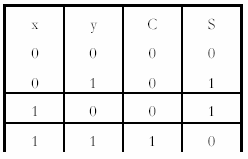
Các Trạng thái Logic của mạch OR
Mạch Hoặc (OR)
Hệ thức Toán học và Ký hiệu
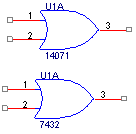 Mạch Hoặc (OR) là một Mạch Logic mà Ngõ ra của nó biến đổi theo các Ngõ vào tuân thủ Hệ thức dưới đây:
Mạch Hoặc (OR) là một Mạch Logic mà Ngõ ra của nó biến đổi theo các Ngõ vào tuân thủ Hệ thức dưới đây:
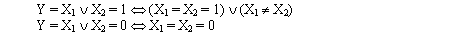
Tức là Ngõ ra của Mạch Hoặc chỉ bằng 0 khi và chỉ khi cả hai Ngõ vào đều bằng 0. Các trường hợp còn lại hoặc chỉ có 1 Ngõ vào bằng 1 hoặc cả hai Ngõ vào đều bằng 1 thì Ngõ ra sẽ bằng 1.
Các loại Vi mạch cơ bản
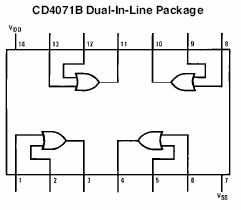
Có hai loại IC rất giống nhau cả về cấu trúc và thứ tự chân đó là 4071 thuộc họ CMOS 4xxx và 7432 (hoặc 74HC32 hoặc 74LS32…) thuộc họ TTL 74xx.
Mỗi IC đều chứa 4 Mạch Hoặc bên trong và có cùng thứ tự chân như nhau nên về nguyên tắc lý thuyết có thể thay thế lẫn nhau. Tuy nhiên Họ CMOS có thể sử dụng được điện áp từ 3V đến 18V còn Họ TTL chỉ sử dụng được điện áp 5V mà thôi.
Hình bên mô tả cấu tạo chung của cả hai loại IC CMOS 4071 và TTL 7432.
l Ứng dụng
Mạch Bán cộng (Half Add)
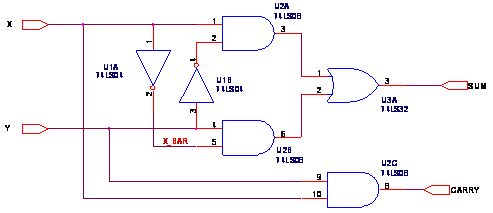
Ứng dụng cơ bản nhất của Mạch Hoặc là phối hợp với các Mạch Logic khác để tạo thành Mạch Bán Cộng: Mạch Bán Cộng là một mạch cộng 2 Bit ở Ngõ vào X và Y sao cho kết quả của phép cộng này là Sum (tổng số kết quả của phép cộng) và Carry (Số nhớ kết quả của phép cộng lên hàng trên kế tiếp theo).
Bản chất của phép cộng này được diễn đạt cụ thể như dưới đây:
Nếu X = Y = 0 thì kết quả tương ứng là Sum = Carry = 0;
Nếu X ≠ Y thì Sum = 1 và Carry = 0;
Nếu X = Y = 1 thì Sum = 0 và Carry = 1
 Vì vậy, nếu X = Y = 0 (hoặc đều bằng 1) thì NotX = NotY = 1 (hoặc đều bằng 0) nên các Ngõ vào của cả hai Mạch AND U2A và U2B đều có 1 Ngõ vào bằng 1 và Ngõ vào kia bằng 0 nên lối ra của 2 Mạch AND đều bằng 0 vì vậy Ngõ ra của Mạch Hoặc U3A cũng bằng 0 tức là Sum = 0;
Vì vậy, nếu X = Y = 0 (hoặc đều bằng 1) thì NotX = NotY = 1 (hoặc đều bằng 0) nên các Ngõ vào của cả hai Mạch AND U2A và U2B đều có 1 Ngõ vào bằng 1 và Ngõ vào kia bằng 0 nên lối ra của 2 Mạch AND đều bằng 0 vì vậy Ngõ ra của Mạch Hoặc U3A cũng bằng 0 tức là Sum = 0;
Chỉ có trường hợp nếu X ≠ Y thì 1 trong 2 Mạch AND nhận được cả 2 Ngõ vào đều bằng 1 nên Sum = 1 và khi đó Carry = X & Y cũng bằng 0.
Duy nhất trường hợp X = Y = 1 thì Sum = 0 (theo giải thích trên đây) và Carry = X&Y = 1 theo đúng các diễn đạt trên đây.
Bảng sự thật trên đây mô tả rõ hơn sự hoạt động của Mạch Bán Cộng nói trên.
Mạch Cộng toàn phần (Full Add)
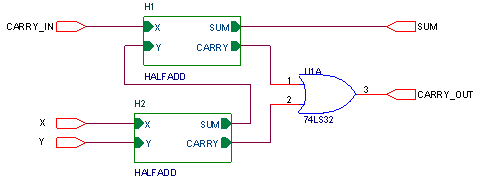
Mạch Bán Cộng trên đây chỉ cho phép thực hiện phép cộng trực tiếp 2 Bit với nhau nhưng không thực hiện được phép cộng có nhớ với kết quả cộng dồn từ các phép cộng đối với các Bit ở hạng thấp hơn nó.
Ví dụ, muốn cộng hai tập Nhị phân A và B có giá trị xác định là A = 1011 và B = 1101 thì phép cộng này phải được tuần tự theo các bước như dưới đây:
Ø Các Bit được phân hạng theo thứ tự nhỏ đến lớn
A B
1 0 1 1 1 1 0 1
a4a3a2a1 b4b3b2b1
Ø Thực hiện cộng các Bit tương ứng
S1 = a1 + b1 và C1 = a1&b1
Trong đó: S1 là kết quả Sum của phép cộng 2 Bit đơn a1 và b1, C1 là số nhớ Carry cho hàng trên kế tiếp theo.
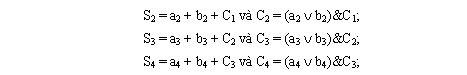
Kết quả của phép cộng nói trên sẽ là:
A + B = S4S3S2S1 và C3
Trên cơ sở dó, Mạch Toàn cộng tối thiểu phải được thiết lập sao cho có thể cộng được trực tiếp 2 Bit ở hạng đang xét với Kết quả nhớ từ phép cộng của Hạng Bit thấp hơn liền kề nó.
Thông qua đó, mạch trên đây được gọi là Mạch Toàn Cộng tối thiếu được tạo bởi 2 Mạch Bán Cộng (Half Add) phối hợp nhau như trên.
l Thiết kế và lắp ráp
Mạch bên đây cho phép tạo ra một Mạch Hoặc có 8 Ngõ vào từ các Mạch Hoặc 2 Ngõ vào cho phép có thể chọn được nhiều Ngõ vào hơn và nhờ đó mở rộng Thuật toán của các Hệ thống Điều khiển lên mạnh hơn và linh hoạt hơn.
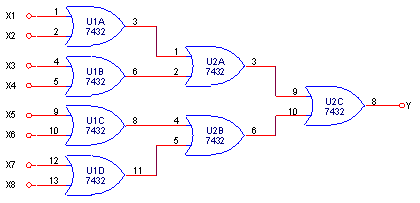
Hoàn toàn có thể tăng hoặc giảm số Ngõ vào bằng cách tăng hoặc giảm các Mạch Hoặc 2 Ngõ vào theo cách phối ghép nói trên.
Tác giả bài viết: Dr Trần Phúc Ánh
Lưu ý: Các bài viết trên in lại các trang web hoặc các nguồn phương tiện truyền thông khác không xác định nguồn http://tri-heros.net là vi phạm bản quyền
Những tin mới hơn
Những tin cũ hơn
 Xem phản hồi
Xem phản hồi Gửi phản hồi
Gửi phản hồi